Go the 4th R in school curriculum

Milton Bradley, an educator organizing the South Huntington Go Program on Long Island, has proposed go as the fourth R, for reasoning, along with the existing three R's in the curriculum at U.S. middle and high schools. Bradley's beliefs are based on reports by leading educators that are exemplified by an article "Tune-ups for the Young Brain" (The New York Times, Feb 11, 1999).

"....educators have been discovering,....that thinking can be taught, and indeed, must be taught. Thinking is a kind of overlord of academia"Arthur Pober, an educational psychologist who conducts workshops nationally on thinking skills, said in the article. "What many grownups don't understand is that learning math and reading, social studies and science, music, woodworking, block building or art doesn't teach youngsters to think. Just the reverse."

Bradley then built on this idea to develop the foundations of his proposal. Even when conventional, education experts agree on the need to incorporate a school subject and teach the process of thinking, Bradley asserts that subject should be called "reasoning." Critical thinking is usually defined as a process ranging from evaluating to inferring logically to hypothesizing. On the other hand reasoning rises above this process by including a process that analyzes a decision-making situation for practical action that is then implemented. Reasoning is therefore the essential meta-skill involved in correctly making the entire complex of everyday decisions that dominate all human interactions, so the ability to effectively utilize it is a primary determinant of each individual's real-world success or failure.

Reasoning and go

Bradley then introduces go. When go is played go well, he said, a set of logical steps is required at each move, which is precisely the same set of logical steps as in the solution of real world problems. But the lessons that go teaches are informal and nonthreatening, in the form of the world's most challenging strategic board game!

One should be suspicious of methods that promise an all-round solution to a topic as pervasive as education. Are all these assertions true? Is reasoning the all-important requisite to better education? Does the game of go incorporate all these steps necessary for reasoning? Let's try to analyze this reasoning procedure in the game between Masao Kato (white) and Rissei O (black) that we started last week.

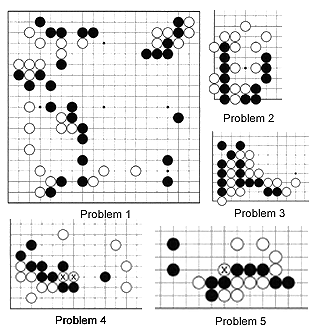
Diagram 1 shows last week's Problem 1. The question was what White would do had Black connected at 1. White at A is only passive as it only takes territory. White B does the same on a larger scale but as an attack it is inadequate. White 1 is the right answer. Rather than concentrating on taking territory, the overriding concern is to isolate the black group from a distance.

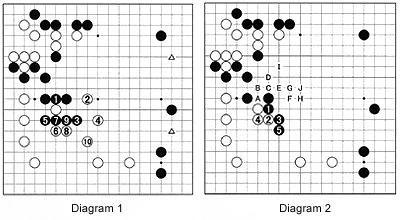
In Diagram 2, the moves to 10 represent five white stones and five black stones. All black stones are inwardly directed while all white stones radiate influence to the outside while profiting on the lower side.

The greater purpose

Thanks to his influence in the center, White can next look forward to invasions at or around the marked spots. This is the result White hoped for, but black 1 to 5 upset his strategy. Black builds thickness with a weak group! This is pure art. But Black has to be concerned about a white cut at A. Black B, White C, Black, D, etc. to I or possibly J could follow. This is clearly bad for Black as he gets cut off and locked up on the left side.

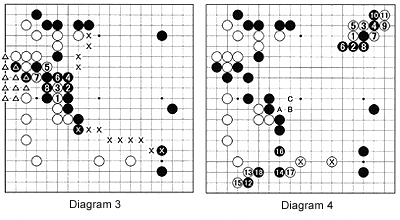
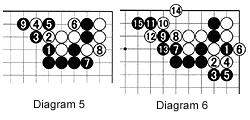
Another variation is shown in Diagram 3. In the sequence to 8, White still has to add a move to secure the left side marked with white triangles, while Black's stones are starting to work in harmony (see the XXX's that start to look like the borders of Black's moyo (framework). Capturing some black stones on such a small scale is useless. In Diagram 4, therefore White plays a do-or-die move at 1 threatening to cut black at A now-if White does so immediately, his stone will be captured in the ladder starting at B. This was Problem 2 of last week. Defending directly at C is too slow and Black would lose too much in the upper right corner. Descending at 3 breaks the ladder, but disregards something that black 2, the move actually played, does not: Black's center strategy. In the sequence to 11, Black sacrifices two stones to not only keep his moyo intact but even expand it. The sacrificed stones 4 and 10 still serve a purpose in expanding Black's influence even more, e.g. Black can force as in Diagram 5 or 6. Returning to Diagram 4, Black can be seen to have many possibilities in the upper right,

so he first wants to find out how White responds to a black threat to the white stones on the lower side. Black 12 forces White to choose between defending the corner at the cost of weakening his two marked stones or strengthen those stones by playing at 18. White chooses to allow Black to cut off the marked stones with 14 and 16. White 17 defends White's base. This is the time that Black has to go back to the basics. He should ask himself what is his main objective. Clearly staying connected is a primary concern, but instead Black allows himself to be seduced by profit and plays 18.

Problems

Problem 1 shows the situation at this point. Keep in mind the theme of connecting your own groups and isolating your opponent's groups to guess where Black should have played and where White will play next. Black plays first in the Problems 2 and 3 to capture cutting stones. Problems 4 and 5 are ladder problems.