Go an educational tool
Last week, U.S. educator Milton Bradley was introduced along with his ideas about including go in the school curriculum. The main reason for this, he asserts, is because go, more than any other popular intellectual game, teaches reasoning skills in an entertaining way. The huge board size of 19x19 lines that offers a total of 361 possibilities for the first move, makes it certain that no two games have ever been played in the same sequence in the game's 4,000-year history. The sheer size of the board makes simultaneous battles on different fronts possible, which can influence each other. A ladder is an example of this. (See Diagram 4.)
In addition to, or rather, due to the sheer number of possibilities, tactics with innumerable variations have to be considered. And eventually, as the skill of the players improves, the fuzzy relationship between the stones will be understood by recognizing shapes and patterns. This process is not so much analytic as intuitive and creative. As they play, children gradually start to understand the relationship between action and result, cause and effect, developing the left hemisphere of the brain.
At the same time, their imagination and creative faculties, which are linked to the right hemisphere of the brain, are stimulated. For example, what we did in last week's game, was to roughly analyze the possibilities-problems and solutions-in specific situations while considering strategy. This is not an accidental activity, but a natural one once people get hooked on go. This process of reasoning and intuitive processing takes place at every level at which the game is played, and becomes increasingly sophisticated as one improves. These considerations all add up to lead one to believe that Bradley was right in proposing that go be included as the fourth 'R' in the school curriculum as it seems to be the best game to provide situations simulating real-life problems that also demand reasoning skills. He also asserts that it is not uncommon for "underachievers" who become captivated by go to become transformed into superior students !
In the real world, one tries to answer such questions as: What is the current situation? What if I do this ? What happens if I do that? How do they compare? Is this an idealized picture of the situation or is it a pessimistic projection? Do outside influences change or they do stay the same? These are questions asked when developing a new product, trying to earn a promotion, solving a human resources problem and when playing go.
Whole board relationships
In Diagram 1, the black 3 in response to white 2 is quite common. Now White has to choose between A and B, both standard responses. The possible variations are endless but Diagram 2 and Diagram 3 are representative of each choice. Diagram 3 involves a ladder. If the ladder is bad, White cannot follow this variation as it gives Black too much influence. If, on the other hand, the ladder is good, White benefit. Under what circumstances is the ladder good for White? If there is a stone in its path, the ladder will be upset. Diagram 4 shows the ladder when played out.
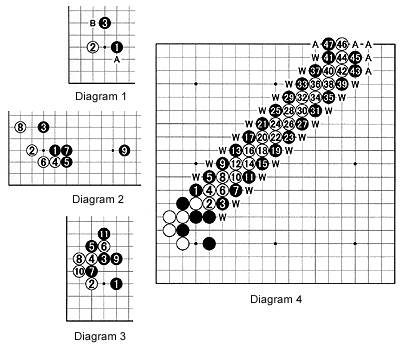
Note that in the last couple of moves of the ladder-Black can change direction a little.
Now if there is a white stone at any place indicated by a 'W', the ladder is broken. Note that a white stone at one of spots marked with an 'A' would not influence the ladder. So in Problems 1 and 2, can White play A, black B, white C ?
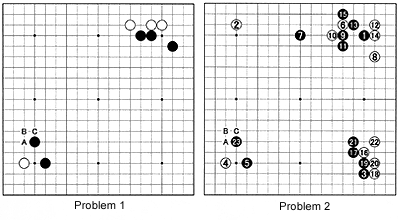
Solutions to last week's problems
Diagram 5, Black has just played the marked stone. White 1 is a kikashi (forcing move) and 3 takes the pivotal point. This move, which strengthens the white group while making territory, aims at an invasion at 21 and also threatens to isolate
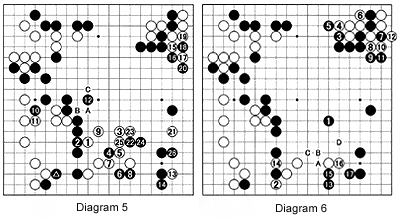
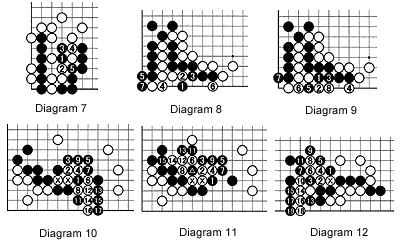
Diagram 6, it is clear that instead of the marked stone, Black should have played at or in the vicinity of 1. Naturally, white 2 follows. Black can now force 3 to 11 to finish his center moyo on the upper right and then come back at 13 to attack White. White 14 defends while profiting but with 15 and 17, Black aims at cutting with black A, white B and black C. If White defends against this cut, Black plays D and secures a lead.
In Diagram 7, black 1 takes the vital point-no matter what White does, some of his stones will be captured. In Diagram 8, Black 1 is the only move. White 2 is natural, but Black now wins the capturing race. In Diagram 9, one's first instinct is black 1 here, but the atari of 2 induces damezumari (shortage of liberties) in Black's shape. Black loses the capturing race by 1 liberty. In Diagram 10 and 11, black 1, 3 and 5 are the winning combination. Resistance by White is futile as these diagrams demonstrate. In Diagram 12, thanks to his two stones on the left, Black can change the direction of the ladder. This type of ladder does not just appear in problems-it also stirs up trouble in actual games.
Problems much more complex than the ones appearing here are omnipresent on the go board at any stage of the game. The only thing you can do to solve problems isthrough lots of practice.
