World chess champion Garry Kasparov met ...
By Rob Van Zeijst
World chess champion Garry Kasparov met his match in 1997 when he played the specially programmed computer Deep Blue. According to some people, go champions will meet the same fate. But even as computers double their speed roughly every 18 months, it is unlikely that computers will be able to play a reasonable game of go in the next 100 years if we only consider the almost infinite number of possibilities in the game. In chess, a computer can make comparisons in the middle game with situations in its endgame library. This is impossible for go because of the sheer number of possibilities. Other problems a computer would face are those involving fuzzy logic, or intuition. In the next few weeks we will include calculation problems, the ones computers can solve but may be difficult for us.
Extensions
We have looked at extensions on the third line. Basically, these serve to ensure life by securing a base or to expand territory on the side. In contrast, extensions on the fourth line generally serve to expand influence.
Diagram 1: In this situation, Black can play at 1 to prevent White from making a shimari (corner enclosure). One possibility for White is attaching at 2. In view of the presence of the marked white stone, the moves through 7 are a natural follow-up. Note Black is trying to settle his group here and therefore a low extension is a safe approach.

Diagram 2: Here the situation is different, because Black has a stone in the lower right. After 5, White may choose the same continuation through 10, but now Black 11 is a good alternative for A as it offers better synergy for Black's stones.
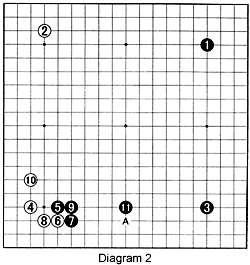
Diagram 3: This strategy of Black playing his first three moves at 1, 3 and 5 on the right is called the sanrensei fuseki, or three-in-a-row opening. In this position, there are very few pros who would choose to play at A, because it does not help Black's center development as much as 5.
Diagram 4: With all Black's stones on the third line and White's on the fourth line, this is an interesting position. Who has more territory? The answer is Black's territory amounts to 136 points against White's 121 points. So Black has 15 points more. You may conclude that the third line is superior to the fourth. However, the number of stones is uneven with 48 white stones and 56 black stones. So in reality, this position can never be achieved. If we look at the efficiency of each stone, each of Black's stones makes 2.43 points per move (136 divided by 56), while White's stones make 2.52 points each (121 divided by 48). As you can see, there is only a difference of 0.09 point per move, but nevertheless, pros call the third line the line of defeat.
Summary: The third line is the line of territory and stability, while the fourth line is for fast development and central influence.

Solution to last week's problem
Solution 1: Black 1 helps White. White will block at 2 and the moves through 7 are natural. Even after 7, Black has a weakness at A as White can cut there. Next, White may want to play at B, or alternatively at C, which would be followed by the sequence black D, white E, black F and white G. Anyway, White's stones at the top are strong after white 2 through 6. That is why Black should refrain from getting too close to White's marked stone and play at A instead of 1.

Problems
Problem 1: It is White's move. Where should he play to capture the three marked stones and set his own marked stone free? There are two solutions, one for beginners and one for advanced players.
Problem 2: This shape resembles the previous problem. The challenge for Black is to make his stones alive. How should he proceed?
Problem 3: White must stabilize his group on the right somehow. The obvious move is in the middle at A or B. This touches vaguely on what we discussed in Diagrams 1 through 3. The issue in this case is about balance. We will discuss this in more detail next week.

Van Zeijst is a four-time European go champion and European representative at the Fujitsu World Championship.
