At the start of each fiscal year on April 1 ...

By Rob Van Zeijst

At the start of each fiscal year on April 1, we traditionally have explained the rules of go. For a game as complex as go, the rules are deceptively simple. A number of Internet sites offer plenty of information for beginners (check out back issues of "The Magic of Go"), so we will only briefly go over the rules this time, before heading into the more appealing aspects of go. The main purpose of go is to obtain more territory than your opponent, but the thrill of the game lies in chasing or bullying your opponent's group, or conversely, saving your stones when you find yourself in a difficult predicament. But remember, a group of stones needs two eyes to survive.

If you want to teach somebody how to play go, it is probably better not to start with your family and closest friends. Start with somebody to whom you have no emotional ties. Without the emotional involvement, you'll have plenty of patience--and that is what you need to be a good teacher.

With friends and especially with family and children, don't assume they will grasp the concepts of go too quickly. Teach by setting small problems to verify what they understand and what they don't. Then challenge them by making it gradually more difficult. If they don't understand a problem, don't tell them the answer; just make it a little easier. All they need is an extra stepping-stone.

Diagram 1: After explaining that Black plays the first move on one of the intersections, I talk about liberties. A stone cannot exist and must be taken off the board if it has no liberties. The sole black stone in the diagram has four liberties, at A, B, C and D. The marked black stone has only one liberty, at E. The marked white stone has no liberties when Black plays at 1 and must be removed from the board.

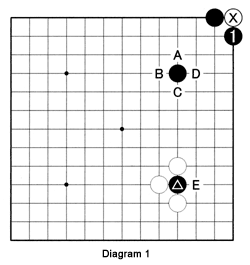
Problem 1: Now look at this problem and work out how many liberties each of the white groups A, B and C have. Note that for the C stones to stay connected, each time Black plays at D, White must answer at E, and vice versa. When you finish this exercise, check Solution 1 to see if you are right.

Problem 2: With the knowledge gained from Problem 1, you can think up situations in which a group of stones cannot be captured. Look at the white group at top left? It has liberties at A and B. If Black plays first, how can he capture these stones? What about the white group at lower right? It appears to have four liberties at C, D, E and F? Play it out on the board and surprise yourself! How many liberties does White have in reality and how should Black go about capturing the white group? Do this exercise on a real board, then check Solution 2.

Problem 3: This is a so-called nakade shape. If Black plays first, the white stones die. Where should Black play? If it is White's turn, where should he play?

Solution to last week's problem

Solution 1A: In response to 1, White must connect at 2. White 4 and 6 are harder to work out. After white 8, the fight seems over, but hold on...

Solution 1B: What if Black connects at 9 and then plays at 11? Well, White just keeps grinding away with 10 and 12, which captures seven stones.

Solution 1C: However, what if Black comes back at 13? White will play at 14 and 16. After black 17, neither White nor Black can move at A or B. Playing for either side is suicide. If White plays, it becomes nakade, a dead shape. You'll find more about this in Solution 2 below.

Solutions to this week's problems

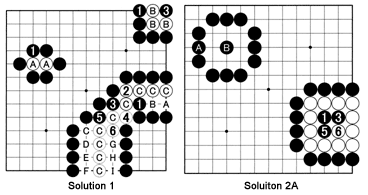
Solution 1: The white stones at A have one liberty at 1. Black 1 therefore captures them. The white stones at B have two liberties. Black must play 1 first--he can't play at 3 immediately because he would be without liberties and that would be suicide, which the rules prohibit--and then at 3. Black 3 takes away White's last liberty and the white group is removed from the board. The stones at C are more complicated. To stay connected, White must answer 1, 3 and 5 with 2, 4 and 6. Now, by counting the number of liberties, A through I, you will find there are nine.

Solution 2A: Black captures the white group with A and B (in that order). This is the result after White's stones are removed from the board. At lower right, Black plays 1, 3 and 5 (White plays elsewhere on the board). However, White now captures three black stones with 6.

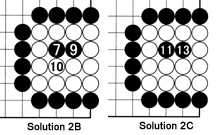
Solution 2B: After the three stones are removed, we get the nakade shape. The correct move for Black is at 7. After White plays elsewhere, Black plays at 9. White again captures at 10.

Solution 2C: After the two black stones are removed, Black comes back once again at 11. This time it is meaningless for White to capture this stone (try this on the board). However, Black can capture the white group on his next turn at 13. Now count all the moves Black and White made and you will find Black needed seven moves against White's two. In other words, Black used five more moves to capture the white group.

Van Zeijst is a four-time European go champion and European representative at the Fujitsu World Championship.