What is the most attractive aspect ...
By Rob Van Zeijst
What is the most attractive aspect of go? When asking a variety of go players, ranging from young to old and from beginner to expert level, the most common answer is that they can use their imagination when playing go. Since the board is empty at the beginning, you can think up positions along with the various responses your opponent may come up with. You can do this in your mind before building the actual position on the board and testing it in the real world. The more resistance you experience, the more you have to use your imagination to come up with better solutions.
However, beginners usually do not know what to think about. There are so many possibilities, it's difficult not to be confused. The best thing is to start out playing on a small nine-by-nine board. Concentrate on one thing at a time. For example, on capturing stones and avoiding being captured. Next, focus on how to make territory, which we will talk about now.
Problem 1: Here are three examples relating to territory. In each case, Black has surrounded nine points of territory. However, in each case the number of stones is different. How many stones did Black use in each case to establish his territory? Which formation is most efficient?
Solution 1 (no diagram): In the top right Black used seven stones, which is the most efficient. In the lower right, he used 11 stones. The least efficient way of making territory is the formation on the left in which Black has used 15 stones.

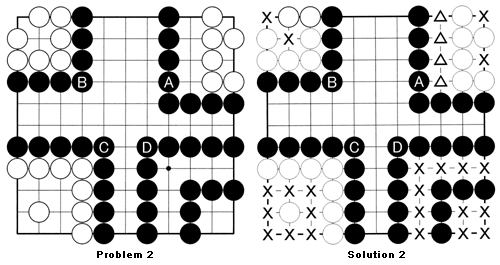
Problem 2: Here are four other formations. In each case A through D, how many points does Black have?
Solution 2: In the cases A through C, Black surrounds White stones. However, in each case White has two eyes and is alive - see Solution 3 in last week's column, for more information on life and death. That means that the spots marked with an X all comprise White territory. White's territory around A is two points, around B, it is two points, and around C, White's territory is eight points. In case D, Black's stones surround 7+4=11 points. What about the points marked with triangles around A? These points are neither surrounded by Black nor White, so they are neutral points, also called dame. Naturally, dame points are worth zero for both parties.
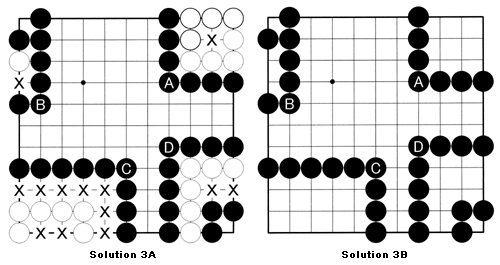
Problem 3: Four more problems. In each case A through D, determine what the status is of the White stones before deciding what Black's territory is in each case. Now, when you decide that some White stones or all of White's stones are dead, take them from the board in each case. The number of points in each case would be the territory gained plus the number of removed stones, called prisoners.

Solution 3A: In each case, Black can occupy the marked spots and in the end take away White's last liberty. White, on the other hand, cannot do anything about it.
Solution 3B: At the end of the game, the players agree which stones are dead and alive (sometimes a stronger player's judgment may be needed). Since White cannot do anything anyway in each case A through D, all of White's stones are removed as shown here. Now you can see, in case A, Black has nine points of territory plus eight prisoners. In other words, Black has 9+8=17 points. In case B, Black has 3+1=4 points. In case C, Black has 15+6=21 points. Finally, in case D, he has 9+6=15 points.
If you got all of these problems right, congratulations!
Solutions to last week's Problem 3
Solution 3A: In case A, black plays 1 and 3 to kill White's group. Last week, we saw why White is dead. In case B, Black plays at 1. White cannot do anything until Black plays at 3. Now White can capture at 4, but Black plays at A on his next turn and we get a similar situation as in case A.
In case C, we get a similar scenario as in case B, so White is dead indeed. The same holds true for case D, which is similar to case A.
Solution 3B: In case A, White makes his space as large as possible by playing at 1. Even if Black plays at 2, White plays at 3 to make two eyes. As you can see, Black cannot play at A or B so White is alive. In case B, White plays at 1 and makes two eyes and is alive.
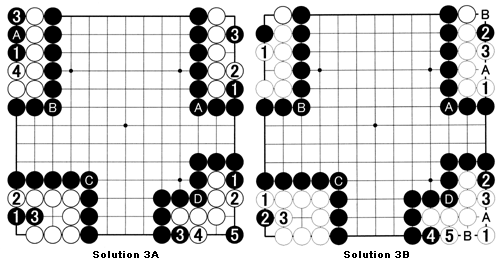
Case C is similar to case A. In case D, white 1 is an elegant solution. Black can try with 2 and 4, but White blocks with 3 and 5 and has two eyes.
Van Zeijst is a four-time European go champion and European representative at the Fujitsu World Championship.
