All novels tell a story. ...

By Rob Van Zeijst

All novels tell a story.Novels that keep us engaged from cover to cover not only have a story--they also have a great plot and often one or more subplots. But the true best sellers offer a quest, a search for a goal with obstacles to be overcome and a powerful reason to keep the pages turning. A good go game also tells a story. Sometimes the game chronicles the rivalry of two contestants from the same generation, or, in the case of the book The Master of Go by Yasunari Kawabata, winner of the 1968 Nobel Prize in Literature, an account of a young player beating the meijin, an allegory for a traditional Japan replaced by a new age with fresh ideas.

In the beginning, your quest is to capture your opponent's stones and avoid being captured in the process. As you progress, look for students to teach as you will learn a lot that way. You will second-guess the things you are learning and search for better and simpler ways of explaining the knowledge you gain, and this will enhance your understanding.

Before starting the lesson, you must realize that if you skip the exercises and just go to the answers, you will only retain about 10 percent of the lesson. It is best to use a go board and stones. Work out the answers on the board and be sure to remove the captured stones. If you are teaching the game, let your students capture and remove those stones. It will make them feel they have accomplished something.

Problem 1: Let's recapitulate on what we learned last week. We talked about stones and groups of stones and their liberties. First, count the liberties of each of White's stones in groups A through E. How many liberties does each group of white stones have? Do the exercises before checking the answers.

Problem 2: The situations in Problem 1 are one-dimensional, because Black is only pursuing White's stones. Now, we get to more complicated problems. A number of black and white stones are in danger of being captured. First, check the status of all the stones. How many liberties do the stones have? Which ones are most important? Try to visualize capturing stones before you play the moves on the go board. Where should Black play if it is his turn?

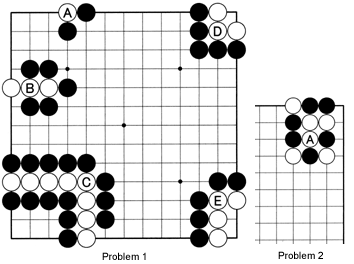
Solution 1 (Note that in all five situations, White's moves are unimportant and have been omitted): White A has one liberty, so it takes only one black move to capture it. Play the move and remove the stone. The stones at white B have two liberties, so Black needs two moves, 1 and 3, to capture the three white stones. The white group of eight stones at C has one liberty. Black 1 occupies that last liberty to capture the White stones. When beginners see situation D, many are confused at first. It seems Black cannot move at 1 because this would leave him without liberties. However, White's stones have only one liberty, and black 1 takes away that last liberty. The white stones around E have two liberties. Black needs two moves to capture them. Technically, White could capture black 1 by playing at 3, but that would be pointless as it would leave White with just one liberty (see Reference 1).

Reference 1: This is the situation in groups A to D after the white stones have been removed from the board. In group E, White has just captured black 1 by playing the marked stone. However, this group now has only one liberty, so Black can capture five stones by playing at 3.

Solution 2A: First, let's count the liberties of each individual stone or group of stones. White A has one liberty, white C one, white E two and white G two. Black B has one, black D two, black F one and black H one. Many stones are in atari, meaning they can be captured on the next move. Now capture each stone or group of stones with just one liberty. As you do that, you find that the worst thing that can happen to White is losing his three stones at A. Why? Because that sets free all of Black's stones.

Solution 2B: So black 1 is the correct move. Take the stones off the board and check that all of Black's stones are safe now.

Last week's problem

This was the problem. Note, White has only two liberties. However, what happens if Black occupies one of these liberties? After checking Reference 2 and 3, you will see this is not the right way for Black to play. Now try again. If it is White's turn, where should he play to stay alive? Alternatively, if it is Black's turn, where should he play to kill White's stones?

Reference 2: If Black occupies either of White's liberties, for example at 1, White will capture that stone. Now look what has happened.

Reference 3: This is the situation after White has captured the black stone. Now Black cannot play at A or B, because neither of these moves takes away White's last liberty. A black stone at A or B cannot exist as it would be without liberties and such a "suicidal" play is prohibited in the rules of go. Compare this with situation D in Solution 1.

Van Zeijst is a four-time European go champion and European representative at the Fujitsu World Championship.