It is common knowledge that the Deep Blue ...

By Rob Van Zeijst

It is common knowledge that the Deep Blue computer beat former world chess champion Garry Kasparov. However, it took computer programmers a long time to achieve this goal. One of the biggest breakthroughs was assigning values to different pieces. Although the value of a piece changes depending on its position, the difference is slight. Thus, exchanges of pieces can be easily evaluated. The problem go programmers face is that the stones only have a value once they are played. During a game, a stone can increase in value or become obsolete.

At the beginning of a game, moves are worth between five and 15 points on average. During the middle game, however, the value of a move can rise to 50 or even more than 100 points as entire groups live or die. The endgame comprises moves starting at around 20 to 25 points and slowly decreasing to two-pointers and, finally, one-pointers.

Diagram 1: Let us have a look at a game between Masaki Ogata, 9-dan, and Shinji Takao, the current Honinbo titleholder, to see how the value of moves changes.

As you can see, the four corners are divided evenly in the first four moves. Let us say these moves each are worth around eight points. Black plays at 5 in the hope of bringing about a development as seen in Reference 1. White 6 counters this. Black 7 aims at monopolizing the right side, but white 8 stops this. Black 9 has multiple functions. First, it attacks by preventing White from making a base. Second, it prevents White from making territory in this area. Third, it is an extension from the top right and makes territory on the right side. This is surely the most valuable move played so far because it has more than one role. This move could easily be worth 20 points. The moves through 17 are joseki (standard moves). Both players aim at making a base here while preventing the opponent from doing so. These moves cannot be evaluated one by one--they should be seen as a combination. According to the QARTS system (Quantitative Analysis of Relative Territory and Strength), a weak group is a liability with a value of minus 20 points. A weak group with one certain eye has a value of minus 10 points, while groups with eyes are worth the value of their territory. In that sense, every move in this area has two purposes: One is to make a base or eyes and the other is to take a base and eyes away from the opponent. In this sense, each move is then worth 20 points+20 points=40 points. However, White and Black play such moves in turn, so they balance each other out. The result up to 24 is that White has a living group with territory of about 10 points and Black has a living group of about six points plus a few stones on the right that aim at annexing the right side. However, they can turn into a weak group. At this moment, the left side looks wider so Black plays at 25.

Reference 1: After 5, if White answers at 6, Black will probably play at 7, a popular strategy these days. If White plays at 8 next, black 9 is just perfect. Black aims at establishing hegemony above and to the right of the marked line in the center.

Diagram 2: At this point, it is important for White to split the marked black stones. Black cannot look after both stones. Black 35 is a superb move. The aim is not to rescue the marked stone, but to eliminate White's potential here (see Reference 2). Destabilizing Black while making territory, white 36 is a great move. Again 37 is a light move--Black is not trying to make a base here. White 38 gains territory that is probably worth around 20 points. Sacrificing his marked stone, Black's real aim is developing the top right with 41 and 45. Note that 37, 39 and 43 contribute to Black's center development. White now has to invade in the top right and 46 through 50 are one way of doing that.

Reference 2: Black 1 is heavy. After white 2, Black has to move into the center. White now has a few options, including capping at F, jumping to G or extending to H. White can always play A, followed by black B, white C, black D, and white E to take away Black's base. Now he has a weak group of minus 10 points. Black is better off giving up his marked stone.

Problems

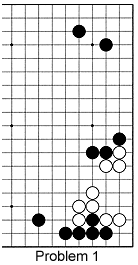
Problem 1: If White were to invade on the right side, how would he go about that? Refer to the QARTS system for a hint.

Problem 2: At the bottom, what moves would make the greatest impact for Black and White, respectively? Again, refer to the QARTS system.

Van Zeijst is a four-time European go champion and European representative at the Fujitsu World Championship.