Is it possible to know how strong the perfect player would be? As a matter of fact, it is. There is a definite correlation between strength and the average difference in score. For example, a game between two beginners could easily average 100 points difference in either direction. The stronger the players get, the smaller the discrepancy tends to be. The average win between two top 9th dans seems to be four to five points.
So to find out what perfect play is, we should look for a difference of zero points. It seems that the perfect player would be about three stones (handicap) stronger than the strongest earthling.
The Last Points
In a way, then, becoming stronger is just a matter of picking up one point here and another there. Imagine you could pick up an extra 10 points in the endgame-would that change your winning percentage ? To tell you a little secret, during teaching games it is not uncommon for White to pick up an extra 20 points in the endgame. When does the endgame start? Usually, it is said to start after all groups are safe.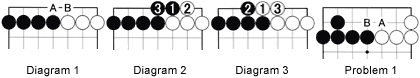
Diagram 1 :
What is the value of a white move at A or a black one at B ?
Diagram 2 :
If Black plays first, he can play the sequence 1 to 3. Locally he gets 3 points to White's 1 point.
Diagram 3 :
If White goes first, he can play the sequence 1 to 3. Locally he gets 2 points to Black's 2 points.
The difference between Diagram 2 and 3 then is 2 points in gote for both players.
Problem 1 :
Here is another gote situation. Either Black or White can play at A, depending on who plays first. How many points is it worth to play there first ?
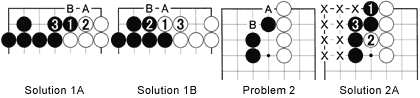
Solution 1A :
If it is Black's turn, he can play moves 1 to 3. Since it's just as likely that Black gets to play at A as White playing at B, we just award each party with half the value. In other words, for calculation purposes imagine that Black plays at B and White at A. Black then has 6 points against White's 1 point, favoring Black by 5 points.
Solution 1B :
Conversely, if White moves first, the following will be the result. As explained above, imagine that White later plays at A and Black at B. The total score is then Black 3 points and White 4 points, favoring White by 1 point.
The difference between Solution 1A and 1B then is 6 points in gote for either player.
For the followup moves of A and B in both solutions, take the mathematical average. We assigned one move that is halfway in between to both parties so that neither can complain. In other words, we gave each player half of the total value of the follow-up which was worth 2 points. Each player therefore gets 1 point.
Problem 2 :
Black can play at A while White has a tesuji at B. How much is playing there worth ?
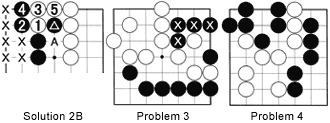
Solution 2A :
If Black defends at 1, White can force 2 for 3. Black now has 9 points (it doesn't matter where you start counting as long as you count from the same place in the alternative possibility-Solution 2B) while we don't count anything for White.
Solution 2B :
Next let's see what happens if White plays at 1. Black's best sequence is shown here. After white 5, Black can decide whether he wants to connect his marked stone with A or not (for example play a move that is worth more than 2 points).
Connecting at A for Black, or the alternative capturing for White, is worth 2 points, but it is gote for both parties. In this case the chance that either player plays at A is 50 percent and we, therefore, give White 1 extra point for this possibility. In other words, Black has 6 points of territory, while White has 1 point (the 50 percent chance of capturing at A to make 2 points).
The difference between these two alternatives is then (Black 9 points in Solution 2A compared to Black 6 points and White 1 point in Solution 2B = 4 points).
Problem 3 :
With just one eye, Black's marked stones seem at a loss. Can you find a tesuji (locally clever move) that turns the tables and wins the game for Black when he plays first ? (komi is 2 points)
Problem 4 :
White to play first and win the game. The first move decides the game immediately.
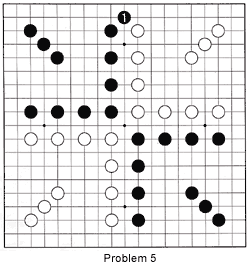
Problem 5 :
In the last few weeks we have talked about sente and initiative. How should White answer black 1 ?
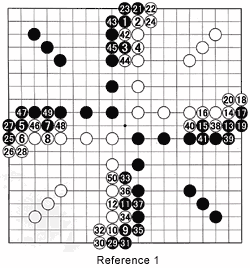
Reference 1 :
This is an unusual position and it would never actually appear on the board, but it perfectly illustrates that just passively returning every move by Black would lose the game for White very easily. For example, if we look at the top formation, after the exchange 1 to 4, 21 to 24 and 42 to 45, Black will have about 3 points more in territory than White (just by counting the top two lines). The same thing happens at the bottom and on the left and right as well, meaning that Black probably leads by 12 points. That's after only about 50 moves, of which half were played by White. White loses half a point for every move he plays.
