Last week, we finally got to the point where we discovered that some groups are so strong they cannot be captured. They are said to be alive.

The second step--part 4

Diagram 1: Here, White has only two liberties but Black can never take away either of these because even if he plays inside White's group, White still has one liberty left, while Black has none.

Diagram 2: Don't confuse this with Diagram 1. Here, White also has two liberties but Black is able to play at either A or B.

Diagram 3: The reason that Black can play at either A or B is that if he plays at 1, he still has a liberty left at A. True, White can capture the black stone by playing at A, but then White would have only one liberty left--where he captured black 1. If White doesn't capture the black stone, he only has one liberty left anyway--at A--and Black can capture the lot by occupying that last liberty.

Life
So what are the characteristics of a group being alive?

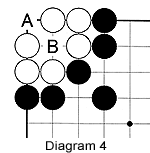
Diagram 4: This white group is alive because Black cannot play at A or B, so he cannot take away White's last liberty. This is similar to Diagram 1.

Eyes
The groups that are alive (Diagrams 1 and 4) have two liberties in separate spaces that we call eyes. Groups with at least two eyes are alive since the last liberty can never be taken away.

Solutions to last week's problems

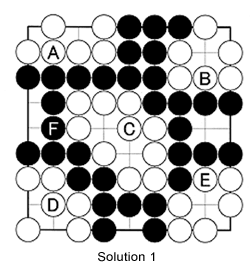
Solution 1: All six groups on the board are alive. Verify for yourself that white groups A through E have two eyes each. Next, check that Black's group is connected everywhere and alive. It has three eyes.

Solution 2A: This situation is more confusing. White's group at A is alive. It has at least two eyes. Black's group B is alive, too, and has two eyes. The white group at C is also alive, with two eyes. Let's discuss the other groups separately.

Solution 2B: This is group D. The marked stone has only one liberty and if Black plays at 1, he will capture it. Then, Black can capture all the White stones with 3.

Solution 2C: Next, is group E. White has two liberties, but not two eyes. If Black plays at 1, White has only one liberty left. But even if he captures with 2, Black comes back inside--at either point--reducing White's liberties to just one.

Solution 2D: F is the last group to consider. White can play at 1, reducing Black's liberties at A to only one. Black has no answer and White can kill by playing at A on his next move.

Now, reconsider groups E and F. Neither is alive, but they are adjacent groups. If Black plays first, he is able to follow Solution 2C, freeing his F group. However, if White moves first he can follow Solution 2D and kill the black group at F, setting his group at E free. In other words, the outcome can be decided by whose turn it is.

Solution 3A: Black A is alive with two eyes at A. White B is alive with two eyes at B. The groups at C and D are more difficult--neither side can play at C. It is a standoff. The groups around E have a similar problem--neither can play at E. What about the black group at F?

Solution 3B: White can capture two stones by playing at 1 (Black would not connect his two stones, as this would leave him with just one liberty).

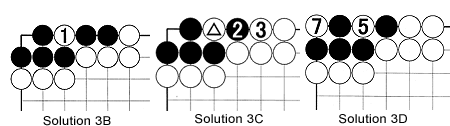
Solution 3C: After White has played the marked stone, Black can recapture with 2. Next, White fills in with 3, putting the stone at 2 in danger. Connecting that stone won't help Black.

Solution 3D: So, if Black does nothing, White can capture with 5, endangering the other black stones. Next, White can capture the lot with 7. Incidentally, this also changes the status of the groups around C, D and E because in the new situation White can kill the black stones in these cases.

Pandanet offers information, lessons The oldest Web site on which go is played is IGS. The site started up in the United States more than 10 years ago. However, it has been acquired by a Japanese company and is now known as pandanet. The address is www.pandanet.co.jp.English/.This is not a free site, but it offers many special events and features professional players who either play demonstration games (with or without commentary) or offer lessons for a fee.

Rob van Zeijst is a four-time European champion and European representative at the Fujitsu World Championship.