The Magic of Go
Ponnuki

Go has a special term--ponnuki--denoting the capturing of a stone in a clean combination of just four moves. This shape can be seen often in beginners' games, but is rarely seen at the professional level. Since it is a basic move, beginners should make it their goal to understand ponnuki, and the move that precedes it--atari.

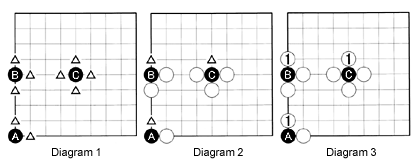
Diagram 1: The three black stones--A, B and C--respectively have two, three and four liberties, represented by the triangles.

These are three separate hypothetical positions for the purpose of showing what happens when a stone in the corner, on the edge or in the center is captured.

Diagram 2: The three black stones each have only one liberty (triangle) remaining, so they are in atari. If White moves next, they can be captured.

Diagram 3: In each case, White 1 completes the capture of the black stone.

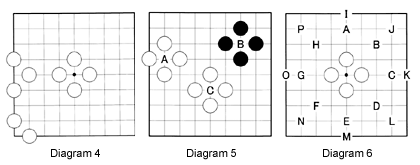
Diagram 4: This is what the end position looks like in each case after the black stones have been captured.

Capturing stones in the corner takes two moves, capturing on the side takes three, and capturing a stone in the center (or at least away from the corner or the side) takes four moves. We refer to the four moves needed in the latter case as ponnuki.

Diagram 5: Here are three ponnuki, where stones have been captured at A, B and C.

Diagram 6: A ponnuki wields considerable influence. It is clear that its power extends all the way from A through H, or even from I through P. On a small board like this (9x9, usually used by beginners), it is possible that Black will not be able to ensure life anywhere on the board. If that is true, it means this particular ponnuki would be worth 81 points--four white stones on the board + one stone captured = 78 points.

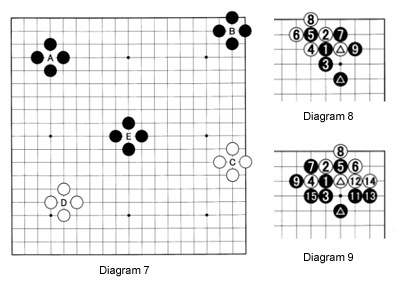
Diagram 7: However, on a regular board (19x19), ponnuki do not generally wield that much influence. Obviously, ponnuki B and C are worth far less than the ones at A, D and E. The ponnuki at B is especially ineffective in that it only has influence on its left and lower sides, while the ponnuki at E could be the most powerful, because it is not hampered in its radiating influence. As a guideline, we say a ponnuki in the center (as in A, D and E) is worth about 30 points.

In each of the ponnuki, one player has invested four moves to capture one stone (one move). The difference is three moves. In other words, a player really plays three moves to score about 30 points, or 10 points per move. That is good, because on average a move is worth about seven to eight points in the beginning.

Diagram 8: After the marked stones have been played, moves 1 through 9 constitute a joseki (standard corner exchange). With 5, Black cuts on what appears to be the wrong side. But this is the way to ensure that he can capture the marked stone. White really has no choice but to capture the cutting stone of 5 by playing at 6 and 8. After black 9, the marked white stone can't escape.

Diagram 9: After white 4, Black could also cut at 5. White needs to capture with 6 and Black sets up a ladder with 7 and 9. Obviously, this variation only works if the ladder is good for Black. White plays 10 elsewhere and Black captures with 15, possibly exchanging 11 and 13 for 12 and 14 first.

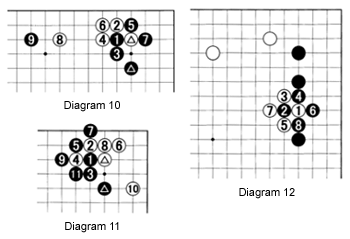
Diagram 10: Sometimes you may feel the urge to connect at 6 instead of capturing black 5. However, this leads to a terrible result. Even after using an extra move at 8, White's stones are not as strong as in Diagram 8. Black 9 is a strong move.

Diagram 11: Likewise, it is not a good idea for White to play at 6, so that he can play at 10 later. Black gets good shape, while White's stones are a little thin. Black's position is far superior, even taking into account an extra move (Black's seven moves versus White's six).

Diagram 12: By now, you understand the power of making a ponnuki. In the same fashion, you shouldn't give away a ponnuki. The situation shown here frequently occurs in handicap games. Often, Black is overwhelmed by White's strength and thinks he is in dire straits after white 1. Sometimes an inexperienced player will try to connect his stones at any cost. And often such a player is proud of the result shown here--after all, he managed to connect his stones and grab a bit of territory in the process.

Problem 1: After white 1 in Diagram 12, can you think of alternatives for black 2? The answer will appear in the next installment of this column.

By Richard Bozulich

By Rob van Zeijst

  1. Example of a pro game
  2. Insight to the pro game
  3. The basics of territory
  4. Be proactive
  5. Take the Initiative
  6. The endgame
  7. The Last Points
  8. Last week's problem
  9. The endgame
  10. Endgame Tesuji
  11. As expected,
  12. Kisei Title
  13. Balancing attack,
  14. Balancing attack and defense
  15. Tobi, kosumi, keima
  16. Tobi, kosumi, keima
  17. The end of the game
  18. O Rissei keeps Kisei title
  19. Solutions to last week's problems
  20. Over the next few weeks
  21. Efficiency calls for good shape
  22. Get an eye for shape
  23. Middle of three stones
  24. Kosumi: pros and cons
  25. Defects of kosumi
  26. Kosumi
  27. Hazama
  28. Attacking
  29. Where there is a keima, there is a cut
  30. Cutting keima the right way
  31. Visualization is a must
  32. Function over form
  33. Rationality
  34. Intuition
  35. Realistic approach
  36. Connecting stones
  37. The so-called cosmic style
  38. Ponnuki
  39. Ponnuki
  40. Ponnuki
  41. Sabotage
  42. Ponnuki and Ko
  43. Fighting ko effectively
  44. Handicap go
  45. Handicap go
  46. The nine-stone handicap
  47. Basics of handicap go
  48. 5 more basic principles of handicap go
  49. Yoda defends Meijin Titlego
  50. Original ideas
  51. The third part of the game
  52. In go, it is easier to...
  53. A good way to improve a game
  54. A big gap between genders
  55. World Championship for Women
  56. Hane defends the Tengen Title
  57. 7-stone handicap
  58. Let's start the New Year...
  59. 9x9 pro game
  60. 9x9 pro game
  61. The following is...
  62. The Go player's...
  63. Of the three most prestigious titles, ...
  64. This is the third installment in a series...
  65. Achallenger has to overcome many obstacles....
  66. In the battle for the 42 million yen.....
  67. Only one week after losing his Kisei.....
  68. After recently losing his Kisei title.....
  69. It is a well-established fact that.....
  70. Go--The first step
  71. Some basics about the pro world
  72. How deep can a pro read?.....
  73. Who are the best go players.....
  74. Can computers play go?.....
  75. Last week, we established.....
  76. Computers have led to a flourishing.....
  77. Though I recommend that you join a go club.....
  78. Last week, we finally got to the point where we discovered that.....
  79. Some people like to offer quotations aimed at showing .....
  80. One of the best and most authoritative Web sites for.....
  81. At the beginner levels, go is an easy game to play.....
  82. We often do things in life without thinking.....
  83. We are often told to do the right thing.....
  84. Following a pattern set by others is easy.....
  85. This week's Go Weekly, a Japanese weekly go newspaper.....
  86. How fast can you do a job and do it right.....
  87. When I am asked by go students how they can.....
  88. Books have been written on the subject.....
  89. Go players are always quick to point out that go is a superior.....
  90. The last few weeks were devoted to tactical issues.....
  91. The fifth and final game in the best-of-five Gosei title match .....
  92. The dividing of land, property, and things of .....
  93. Fireworks are expected between current Meijin .....
  94. Dividing land, property or living space in one's own favor is .....
  95. The dream match between the current Kisei .....
  96. Three games have now been completed in the best-of-seven series.....
  97. We have talked strategy over the past few weeks.....
  98. In study, in all branches of sport.....
  99. The most important things a go beginner.....
  100. In many games and sports,.....
  101. How do you do confront your fears?.....
  102. In go, you cannot expect to deal with.....
  103. When your opponent is much stronger than you.....
  104. Using the power of your opponent for.....
  105. The combination of aggressiveness, .....
  106. Last week, there was some good news for.....
  107. On Dec. 18, in the fifth game of.....
  108. Go Weekly, which hits the nation's newsstands every Monday.....
  109. In go, the beginner must try to master the basics of life and.....
  110. Last week, we started a new series on life and.....
  111. This is the third article in a series on life-and.....
  112. In this article, the fourth in a series, we will take.....
  113. This is the fifth installment of tsume go.....
  114. Practice, practice, practice. This is the way to improve.....
  115. The Kisei title match, worth more than $400,000.....
  116. The Kisei title match, worth more than $400,000.....
  117. For a champion, 25-year-old Keigo Yamashita has.....
  118. In two-day best-of-seven matches.....
  119. Naoki Hane has iron nerves.....
  120. The game of go can be as easy or as difficult.....
  121. On April 18 and 25, the TV Tokyo network will.....
  122. Give and take is widely used in daily life to strike.....
  123. Although go has a history of almost 4,000 years.....
  124. The adage "Chess was invented but go was discovered".....
  125. Unlike chess, in which a board position.....
  126. Over the past few weeks we have concentrated.....
  127. Go is sometimes perceived as a more difficult game than chess
  128. Last week, I stressed that the objective of go was to.....
  129. Anyone can learn the basics of go.
  130. Go can be considered a zero-sum game as .....
  131. If you play a strategic game like go, taking or keeping .....