Going by the dictionary definition, intuition and rationality would seem to be mutually exclusive, but in my view, we can become more intuitive by using logic and rationality. Last week, we took a look at the fundamentals of the QARTS (Quantitative Analysis of Relative Territory and Strength) system, which I created as a tool to assess position and get a feel for what part of the board is important, which stones need reinforcement and which ones should be abandoned. We concentrated on invasions and their value. This time, we will focus on positions that already have a base.
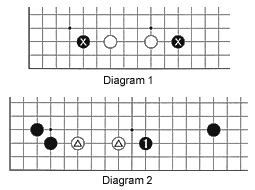Diagram 1: The white stones have a base, but how strong is it when bracketed by the marked black stones? And by extension, what would the value then be of either or both of the marked black stones?
Diagram 2: The white stone position is the same, but the black configuration is slightly different. Should Black play at 1 early on, or should he play elsewhere?
Diagram 3: This situation occurs frequently. The fuseki (opening) strategy to 7 is commonly employed and one of my favorites when playing Black. A white approach at 8 is also common in response. Black 9 initiates a joseki (standard corner exchange) in which white 10 is the usual move. The question is should Black now play at A or B?
Diagram 4: If Black prevents a white shimari in this area by playing at 1, the moves to 10 are a possible continuation. The exchange white 8 for black 9 strengthens the marked white stones even if it does not prevent a black invasion at A. However, it will be White who takes the initiative in that case--after all if Black plays at A, White's stones form a 3 to 1 material majority. Somehow, it looks as if White got the better part of the deal.
Diagram 5: On the other hand, if Black starts an attack with 1 to confine the marked white stones, a continuation to 13 as shown here is a possibility.
First of all, black 1 induces the white jump to 2, allowing Black to make territory naturally with 5. White makes a shimari with 6 and Black extends to 7 (while limiting the extension possibilities of the white shimari). White 8 seems a natural invasion, but black 9 profits in aggressively denying White a base in the corner. Black 13 relieves pressure on his own group while keeping pressure on the white group.
White then has two relatively weak groups (8, 10 and 12 and the group with the marked stones), making it difficult to invade at A or B as this would create a third weak group. In retrospect, black 1 pressures the marked stones and allows him to make territory on both the lower side and in the upper right.
How does this really work?
Problem 1: What is the value of black 1? Use the QARTS system, in which weak groups without eyes are valued at 20 and those with just one eye are valued at zero to minus 10 points (depending on the ability to make territory).
Problem 2: Where should Black play? Can you give a quantitative reason?
Problem 3: Locally, where should Black play? Once more, justify your answer using the QARTS system.
Solution 1A: To work out the answer to Problem 1, we need to compare a couple of alternatives. Let's first assume that White ignores Black's move. Black can follow up with the sequence to 10. Black has now built up a large center framework and increased the value of this territory by at least 20 points.
Furthermore, he has secured the upper right corner, which compares favorably to a possible exchange of white A for black B (if Black hadn't played the marked stone), and increased his territory in the marked area (about 8 points). On the other hand, White made a few points with his group (about 8 points).
Overall, this tilts the balance in Black's favor by at least 20 points--the number of stones in this diagram is the same for Black and White, so the positive balance is entirely due to the marked black stone.
Solution 1B: What if White did answer the marked Black stone? Then Black would still get the marked points in the upper corner and he would probably defend at 5, which also makes points. Black has increased the value of this territory by at least 10 points, plus the territory in the upper right (8 points) against White's 6 points, for a total of 12 points in Black's favor.
Solution 1C: Here is the situation if Black doesn't play at 1 in Problem 1. Then White would probably slide into the corner with 1. Black 2* is big--it enables him to play the sequence black A, white B, etc., and in the end capture white 1 with black 1. But even that would leave the marked white stones stronger.
White 1 makes the corner smaller by at least 8 points in sente but it also strengthens the marked stones, changing the status from a weak group of about zero points to a strong group with more than 10 points in territory and a possible invasion at K (worth another 10 points or so).
The differences between Solutions 1A, 1B and 1C should be fully assessed. But, as you see when you start assigning points for strengths and weaknesses, it quickly becomes too difficult to make an accurate assessment.
At the same time, it gives you a good idea of the real value of black 1 in Problem 1 or white 1 in Solution 1C. The difference could easily be 20 to 30 points (depending on surrounding circumstances).
* To be really fair, we should consider the possibility that Black plays somewhere else, which means White would have the opportunity to march even farther into the corner--that is also part of the value of white 1 here.
Next week, we will discuss Problems 2 and 3. Make diagrams similar to the solution diagrams for Problem 1. Try to put a rough value on a move instead of vague qualifications such as "large" or "small." After some practice, it will help you develop a feel for the value of moves, which in turn will make you more intuitive.