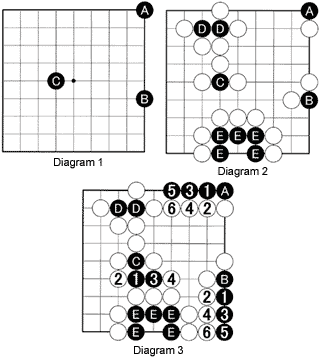
Diagram 1: Can you see how many liberties each of Black's stones A, B and C have? A obviously has the fewest with two, while B has three and C has four.
Diagram 2: How many liberties do A, B and C have now? And what about the D and E groups? All of Black's stones are in atari because they have only one liberty. In other words, they are in danger of being captured on the next move. And what is more, there is no escape. With the groups D and E, this is obvious as it is impossible for Black to increase his liberties. A, B and C can attempt to do so but any move Black makes would be immediately countered by White.
Diagram 3: If Black tries to save A by playing at 1, White will simply answer with 2. After white 6 it becomes obvious Black has nowhere to go. Black B is also on the 1st line and any effort to escape would be countered. White 6 would capture four black stones. If Black tries to save C, he will end up losing three stones when white 4 is played.
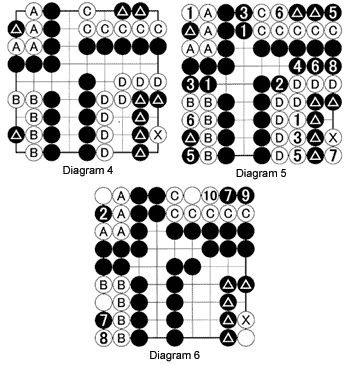
Diagram 4: The white groups A through D are surrounded. The A group has only one liberty. In the other groups, White cannot increase his liberties. However, the white stones themselves enclose black stones. White group D, for example, surrounds five marked black stones. What is the status of these groups? Who can capture whom?
Diagram 5: When considering the status of a group, we should consider what happens if it is Black's turn to play or if White plays first. If Black moves first against the A group, he can capture four white stones, but if White plays first, he can capture one stone. What happens next?
White can capture one stone in the case of B. But what if he does not do this? Black 1 will take away one of White's liberties, and if White plays elsewhere, black 3 will cancel out another one. If Black then plays at 5, White can capture two stones with 6. What happens next?
The C group situation is similar to that of the B group. What happens after White captures three stones with 6?
The D situation is more straightforward. If White starts taking away liberties with 1, 3 and 5, Black does the same with 2, 4 and 6 to put White in atari. White does the same with 7, but Black 8 captures 11 white stones.
Diagram 6: In the case of A, Black can capture five white stones by playing at 2. If Black plays at 7 in the case of B, White can capture it with 8. But if he does, he will lose seven stones. In the C group, Black can play inside with 7. White cannot really answer this but if he plays elsewhere, Black will play at 9. If White captures the two stones with 10, the outcome will be similar to that of the B scenario. In the final group, the result can be seen after the D stones have been removed. In the cases of A, B and C, Black sacrifices some stones in order to capture more white stones.
Solution to last week's problems
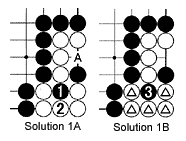Solution 1A: Black 1 is a surprise move. White can capture at 2 or at A, but these moves would not accomplish anything. Let's look what happens after white 2.
Solution 1B: This is the situation. The five marked stones are in atari and it is Black's turn. So Black can play at 3 and capture the marked stones. This technique of throwing in a stone to capture more stones is called a snapback. Note that this does not repeat a board situation and is therefore permissible.
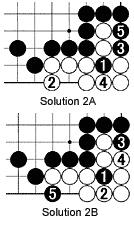Solution 2A: Black 1 is unexpected. White 2 makes an eye but black 3 puts him on the spot. White 4 is necessary but if he plays at 5, it becomes a snapback. After black 5, the white stones are dead.
Solution 2B: Alternatively, White can play at 2 and 4 to make an eye, but black 5 takes away the other eye. So White dies anyway.
New Problems
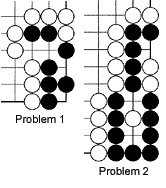Problem 1: How can White capture Black's stones?
Problem 2: White can set up a snapback. How?
Want to find out more? Come to Ben's Cafe (03-3202-2445) in Takadanobaba, Tokyo, where the English speaking go community congregates every Sunday. You can enjoy free lessons, 11 a.m.-1 p.m. Ben's Cafe can be accessed at www.benscafe.com.
Van Zeijst is a four-time European go champion and European representative at the Fujitsu World Championship.