Can computers play go? Yes, they can, but only at a rudimentary level. A zealous beginner who plays every day probably would be able to beat the best computer programs in the world in about a year. One of the problems is that computer programs do not take into account the value of each stone. The value of a stone depends on how well it works with other stones. However, stones can hamper each other and reduce the value of stones nearby. Unlike chess, where calculations are clear-cut because the pieces pretty much have fixed values and the board is fairly small, it is more difficult for computers to make precise calculations in go. However, go highlights what human beings are good at--making and changing plans, flexibility and fuzzy reading.

The first step--part 5

For the past two weeks we have been investigating ways to snare stones and to make sure they cannot escape. One technique we looked at was the ladder, which involves keeping stones down to one liberty with each turn. This week we will look at "nets"--another way of making sure a stone, or multiple stones, cannot escape.

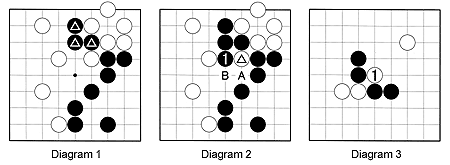
Diagram 1: The marked black stones are in a little trouble. How can they connect to the main group?

Diagram 2: Black 1 makes sure the marked white stone cannot escape. For example, if White plays at A, Black captures two stones with B. The marked stone is caught in a net.

Diagram 3: White 1 is an aggressive move as it cuts the black stones into two groups. However, it is overly aggressive because it is too far away from the white stone at upper right. Black can catch the white stone by using a net. How does that work?

Diagram 4: After white 1, black 2 is the best move. This ensures white 1 cannot escape. What happens if White tries to escape? The only ways out are 3 and 5. However, Black keeps White inside by closing the net with 4 and 6, capturing three white stones.

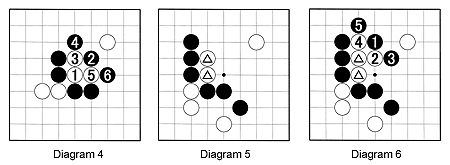
Diagram 5: The marked white stones are cutting Black's stones in two. Fortunately, it is possible to capture them. How can Black do this?

Diagram 6: Black 1 is the correct move. If White tries to escape, with 2 and 4, for example, the net becomes tighter and with every move, White loses a liberty.

Solutions to last week's problems

Solution 1: The question was, can Black ensure the capture of white A? Black 1 is correct. If White does not answer, Black can capture by playing at 2. What happens if White tries to escape with 2? Black again reduces White's liberties to one by playing at 3. White 4 is a bad move as black 5 captures three stones. The best thing for White to do is abandon his stone at A.

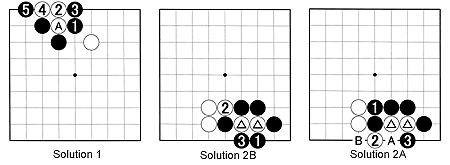
Solution 2A: Black 1 ensures the capture of the marked white stones. If White tries to connect with 2, black 3 makes clever use of White's shortage of liberties. White will be captured next if he does not play at A. But if he does, Black plays at B and captures four white stones.

Solution 2B: Black has other ways of ensuring the capture of the marked white stones: he can also play at 1. If White plays at 2, black 3 captures the marked stones.

Solution 3: The question asked was whether Black could capture the marked stone by playing at 1. White 2 is the only way to escape, but black 3 through 11 keeps White's liberties down to just one. Even if White plays at A, he cannot escape. Black captures by playing at B. So the answer is yes--black 1 will eventually capture the marked white stone. And, of course, White should not try to escape as this will only cause more damage.

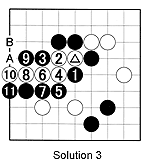
New Problems

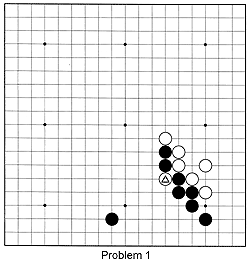Problem 1: This position is from a pro game that was played during the Fujitsu tournament. Where should Black play to capture the marked white stone?

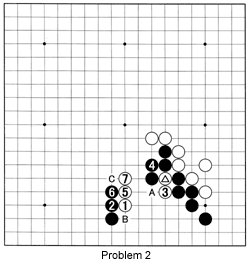
Problem 2: In the same game, a few moves later, White cleverly saved the marked stone through the combination of 1 and 3. Black was forced to connect with 4. After white 7, White threatens to connect with A. In the game, after white 7, Black caught the marked stone and white 3 using a net. How did he do that?

Next week, you can find the answers to these problems, or you can find out tomorrow at Ben's Cafe in Takadanobaba (03-3202-2445 or www.benscafe.com), where the English-speaking go community gathers every Sunday at 11 a.m. You can enjoy free lessons until 1 p.m.

Rob van Zeijst is a four-time European champion and European representative of the Fujitsu World Championship.